Show Mobile Notice

1. Derivative Of Arctan(3x)
2. Derivative Calculator
3. Derivative Of Arctan Calculator
4. Derivative Of Arctan
5. Derivative Of Arctanx/3

Show All Notes

Below is shown arctan(tan(x)) in red and its derivative in blue. Note that the derivative is undefined for values of x for which cos(x) is equal to 0, which means at x = π/2 + k. Π, where k is an integer. The inverse tangent — known as arctangent or shorthand as arctan, is usually notated as tan-1 (some function). To differentiate it quickly, we have two options: 1.) Use the simple derivative rule. 2.) Derive the derivative rule, and then apply the rule. In this lesson, we show the derivative rule for tan-1 (u) and tan-1 (x). The Derivative of Arctan x. If y = tan-1 x, then tan y = x. Taking the derivative of the second expression implicitly gives: solving for the derivative gives: (1). Derivative of arctan(x) Let’s use our formula for the derivative of an inverse function to find the deriva­ tive of the inverse of the tangent function: y = tan−1 x = arctan x. We simplify the equation by taking the tangent of both sides. The Derivative of an Inverse Function. We begin by considering a function and its inverse. If (f(x) ) is both invertible and differentiable, it seems reasonable that the inverse of (f(x) ) is also differentiable.

Hide All Notes

Section 3-7 : Derivatives of Inverse Trig Functions

In this section we are going to look at the derivatives of the inverse trig functions. In order to derive the derivatives of inverse trig functions we’ll need the formula from the last section relating the derivatives of inverse functions. If (fleft( x right)) and (gleft( x right)) are inverse functions then,

[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}}]

Recall as well that two functions are inverses if (fleft( {gleft( x right)} right) = x) and (gleft( {fleft( x right)} right) = x).

We’ll go through inverse sine, inverse cosine and inverse tangent in detail here and leave the other three to you to derive if you’d like to.

Inverse Sine

Let’s start with inverse sine. Here is the definition of the inverse sine.

[y = {sin ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}sin y = xhspace{0.25in}{mbox{for}}, - frac{pi }{2} le y le frac{pi }{2}]

So, evaluating an inverse trig function is the same as asking what angle (i.e. (y)) did we plug into the sine function to get (x). The restrictions on (y) given above are there to make sure that we get a consistent answer out of the inverse sine. We know that there are in fact an infinite number of angles that will work and we want a consistent value when we work with inverse sine. Using the range of angles above gives all possible values of the sine function exactly once. If you’re not sure of that sketch out a unit circle and you’ll see that that range of angles (the (y)’s) will cover all possible values of sine.

Note as well that since ( - 1 le sin left( y right) le 1) we also have ( - 1 le x le 1).

Let’s work a quick example.

Example 1 Evaluate (displaystyle {sin ^{ - 1}}left( {frac{1}{2}} right)) Show Solution

So, we are really asking what angle (y) solves the following equation.

[sin left( y right) = frac{1}{2}]

and we are restricted to the values of (y) above.

From a unit circle we can quickly see that (y = frac{pi }{6}).

We have the following relationship between the inverse sine function and the sine function.

[sin left( {{{sin }^{ - 1}}x} right) = xhspace{0.5in}{sin ^{ - 1}}left( {sin x} right) = x]

In other words they are inverses of each other. This means that we can use the fact above to find the derivative of inverse sine. Let’s start with,

[fleft( x right) = sin xhspace{0.5in}gleft( x right) = {sin ^{ - 1}}x]

Then,

[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{cos left( {{{sin }^{ - 1}}x} right)}}]

This is not a very useful formula. Let’s see if we can get a better formula. Let’s start by recalling the definition of the inverse sine function.

[y = {sin ^{ - 1}}left( x right)hspace{0.5in} Rightarrow hspace{0.5in}x = sin left( y right)]

Using the first part of this definition the denominator in the derivative becomes,

[cos left( {{{sin }^{ - 1}}x} right) = cos left( y right)]

Now, recall that

[{cos ^2}y + {sin ^2}y = 1hspace{0.5in} Rightarrow hspace{0.5in}cos y = sqrt {1 - {{sin }^2}y} ]

Using this, the denominator is now,

[cos left( {{{sin }^{ - 1}}x} right) = cos left( y right) = sqrt {1 - {{sin }^2}y} ]

Now, use the second part of the definition of the inverse sine function. The denominator is then,

[cos left( {{{sin }^{ - 1}}x} right) = sqrt {1 - {{sin }^2}y} = sqrt {1 - {x^2}} ]

Putting all of this together gives the following derivative.

[frac{d}{{dx}}left( {{{sin }^{ - 1}}x} right) = frac{1}{{sqrt {1 - {x^2}} }}]

Inverse Cosine

Now let’s take a look at the inverse cosine. Here is the definition for the inverse cosine.

[y = {cos ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}cos y = xhspace{0.25in}{mbox{for}},0 le y le pi ]

As with the inverse sine we’ve got a restriction on the angles, (y), that we get out of the inverse cosine function. Again, if you’d like to verify this a quick sketch of a unit circle should convince you that this range will cover all possible values of cosine exactly once. Also, we also have ( - 1 le x le 1) because ( - 1 le cos left( y right) le 1).

Example 2 Evaluate (displaystyle {cos ^{ - 1}}left( { - frac{{sqrt 2 }}{2}} right)). Show Solution

As with the inverse sine we are really just asking the following.

[cos y = - frac{{sqrt 2 }}{2}]

where (y) must meet the requirements given above. From a unit circle we can see that we must have (y = frac{{3pi }}{4}).

The inverse cosine and cosine functions are also inverses of each other and so we have, [cos left( {{{cos }^{ - 1}}x} right) = xhspace{0.5in}{cos ^{ - 1}}left( {cos x} right) = x]

To find the derivative we’ll do the same kind of work that we did with the inverse sine above. If we start with

[fleft( x right) = cos xhspace{0.5in}gleft( x right) = {cos ^{ - 1}}x]

then,

[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{ - sin left( {{{cos }^{ - 1}}x} right)}}]

Simplifying the denominator here is almost identical to the work we did for the inverse sine and so isn’t shown here. Upon simplifying we get the following derivative.

[frac{d}{{dx}}left( {{{cos }^{ - 1}}x} right) = - frac{1}{{sqrt {1 - {x^2}} }}]

So, the derivative of the inverse cosine is nearly identical to the derivative of the inverse sine. The only difference is the negative sign.

Inverse Tangent

Here is the definition of the inverse tangent.

[y = {tan ^{ - 1}}xhspace{0.5in} Leftrightarrow hspace{0.5in}tan y = xhspace{0.25in}{mbox{for}}, - frac{pi }{2} < y < frac{pi }{2}]

Again, we have a restriction on (y), but notice that we can’t let (y) be either of the two endpoints in the restriction above since tangent isn’t even defined at those two points. To convince yourself that this range will cover all possible values of tangent do a quick sketch of the tangent function and we can see that in this range we do indeed cover all possible values of tangent. Also, in this case there are no restrictions on (x) because tangent can take on all possible values.

Example 3 Evaluate ({tan ^{ - 1}}1). Show Solution

Here we are asking,

[tan y = 1]

where (y) satisfies the restrictions given above. From a unit circle we can see that (y = frac{pi }{4}).

Because there is no restriction on (x) we can ask for the limits of the inverse tangent function as (x) goes to plus or minus infinity. To do this we’ll need the graph of the inverse tangent function. This is shown below.

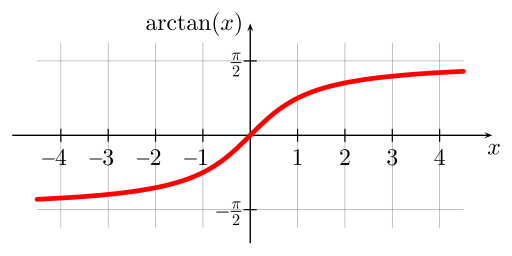
From this graph we can see that

[mathop {lim }limits_{x to infty } {tan ^{ - 1}}x = frac{pi }{2}hspace{0.5in}hspace{0.25in}mathop {lim }limits_{x to - infty } {tan ^{ - 1}}x = - frac{pi }{2}]

The tangent and inverse tangent functions are inverse functions so,

[tan left( {{{tan }^{ - 1}}x} right) = xhspace{0.5in}{tan ^{ - 1}}left( {tan x} right) = x]

Therefore, to find the derivative of the inverse tangent function we can start with

[fleft( x right) = tan xhspace{0.5in}gleft( x right) = {tan ^{ - 1}}x]

We then have,

[g'left( x right) = frac{1}{{f'left( {gleft( x right)} right)}} = frac{1}{{{{sec }^2}left( {{{tan }^{ - 1}}x} right)}}]

Simplifying the denominator is similar to the inverse sine, but different enough to warrant showing the details. We’ll start with the definition of the inverse tangent.

[y = {tan ^{ - 1}}xhspace{0.5in} Rightarrow hspace{0.5in}tan y = x]

The denominator is then,

[{sec ^2}left( {{{tan }^{ - 1}}x} right) = {sec ^2}y]

Now, if we start with the fact that

[{cos ^2}y + {sin ^2}y = 1]

and divide every term by cos² (y) we will get,

[1 + {tan ^2}y = {sec ^2}y]

The denominator is then,

[{sec ^2}left( {{{tan }^{ - 1}}x} right) = {sec ^2}y = 1 + {tan ^2}y]

Finally using the second portion of the definition of the inverse tangent function gives us,

[{sec ^2}left( {{{tan }^{ - 1}}x} right) = 1 + {tan ^2}y = 1 + {x^2}]

The derivative of the inverse tangent is then,

[frac{d}{{dx}}left( {{{tan }^{ - 1}}x} right) = frac{1}{{1 + {x^2}}}]

There are three more inverse trig functions but the three shown here the most common ones. Formulas for the remaining three could be derived by a similar process as we did those above. Here are the derivatives of all six inverse trig functions.

We should probably now do a couple of quick derivatives here before moving on to the next section.

Example 4 Differentiate the following functions.

1. (fleft( t right) = 4{cos ^{ - 1}}left( t right) - 10{tan ^{ - 1}}left( t right))
2. (y = sqrt z , {sin ^{ - 1}}left( z right))

Show All SolutionsHide All Solutionsa (fleft( t right) = 4{cos ^{ - 1}}left( t right) - 10{tan ^{ - 1}}left( t right)) Show Solution

Not much to do with this one other than differentiate each term.

[f'left( t right) = - frac{4}{{sqrt {1 - {t^2}} }} - frac{{10}}{{1 + {t^2}}}]
b (y = sqrt z , {sin ^{ - 1}}left( z right)) Show Solution

Don’t forget to convert the radical to fractional exponents before using the product rule.

[y' = frac{1}{2}{z^{ - frac{1}{2}}}{sin ^{ - 1}}left( z right) + frac{{sqrt z }}{{sqrt {1 - {z^2}} }}]

Alternate Notation

There is some alternate notation that is used on occasion to denote the inverse trig functions. This notation is,

[begin{array}{ll}{sin ^{ - 1}}x = arcsin x & hspace{1.0in}{cos ^{ - 1}}x = arccos x {tan ^{ - 1}}x = arctan x & hspace{1.0in}{cot ^{ - 1}}x = {mbox{arccot }}x {sec ^{ - 1}}x = {mathop{rm arcsec}nolimits} ,x & hspace{1.0in}{csc ^{ - 1}}x = {mathop{rm arccsc}nolimits} ,xend{array}]

Derivative Of Tangent – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. Common trigonometric functions include sin(x), cos(x) and tan(x). For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a). f ′(a) is the rate of change of sin(x) at a particular point.

All derivatives of circular trigonometric functions can be found using those of sin(x) and cos(x). The quotient rule is then implemented to differentiate the resulting expression. Finding the derivatives of the inverse trigonometric functions involves using implicit differentiation and the derivatives of regular trigonometric functions.

Derivative Of Tangent

To find the derivative of a tangent of x, we’ll start by writing tan x as sin x/cos x and then use the quotient rule to differentiate.

The quotient rule says that if two functions are differentiable, then the quotient is also differentiable. Here’s the quotient rule applied to tan x when in form of sin x/cos x

Now we know that the derivative of sin x is cos x and the derivative of cos x is -sin x. Substituting these derivatives in the parentheses and simplifying, we get

Now there are two trigonometric identities we can use to simplify this problem

• sin²x + cos²x = 1
• sec x = 1/cos x

And that’s it, we are done! The derivative of tan x is sec²x.

However, there may be more to finding derivatives of the tangent. In the general case, tan x is the tangent of a function of x, such as tang(x). Note in the simple case, g(x) = x.

Derivative Of Arctan(3x)

Generally, we are looking for

Derivative Of Inverse Tangent

The following are the formulas for the derivatives of the inverse trigonometric functions

We let y=arctan x

Where

Then

tan y=x

Using implicit differentiation and solving for dy/dx:

Left side

Right side

Therefore,

Substituting x=tany in from above, we get

Slope Of Tangent Line Derivative

Tangent Lines

The first problem that we’re going to take a look at is the tangent line problem. Before getting into this problem it would probably be best to define a tangent line.

A tangent line to the function f(x)f(x) at the point x=ax=a is a line that just touches the graph of the function at the point in question and is “parallel” (in some way) to the graph at that point. Take a look at the graph below.

Derivative Calculator

In this graph, the line is a tangent line at the indicated point because it just touches the graph at that point and is also “parallel” to the graph at that point. Likewise, at the second point shown, the line does just touch the graph at that point, but it is not “parallel” to the graph at that point and so it’s not a tangent line to the graph at that point.

At the second point shown (the point where the line isn’t a tangent line), we will sometimes call the line a secant line.

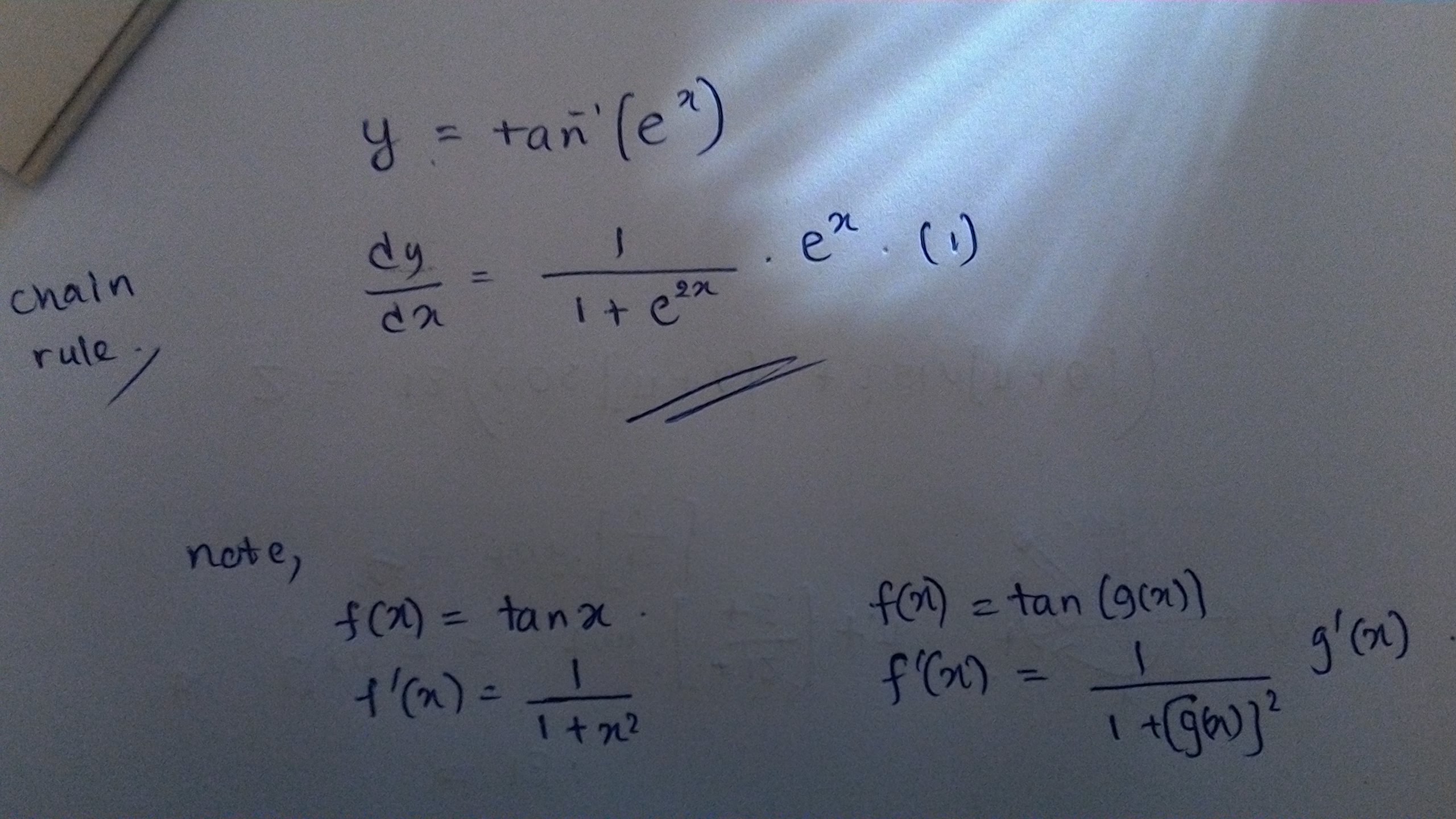
We’ve used the word parallel a couple of times now and we should probably be a little careful with it. In general, we will think of a line and a graph as being parallel at a point if they are both moving in the same direction at that point. So, in the first point above the graph and the line are moving in the same direction and so we will say they are parallel at that point. At the second point, on the other hand, the line and the graph are not moving in the same direction so they aren’t parallel at that point.

Derivative Of Arctan Calculator

Okay, now that we’ve gotten the definition of a tangent line out of the way let’s move on to the tangent line problem.

Derivative Of Arctan

What Are The Derivative Of Tangent?

Derivatives Of Trigonometric Functions. The Basic Trigonometric Functions Include The Following 6 Functions: Sine (Sinx), Cosine (Cosx), Tangent (Tanx), Cotangent (Cotx), Secant (Secx) And Cosecant (Cscx). All These Functions Are Continuous And Differentiable In Their Domains.

Derivative Of Arctanx/3

What Is Derivative Of Tangent, An Inverse Tangent?

The Arctangent Of X Is Defined As The Inverse Tangent Function Of X When X Is Real (X∈ℝ). When The Tangent Of Y Is Equal To X: Tan Y = X. Then The Arctangent Of X Is Equal To The Inverse Tangent Function Of X, Which Is Equal To Y: Arctan X= Tan-1 X = Y.

What Is The Derivative Of Sin2X?

Namely, Dy/Dx= 2*Cos(2X). Remember That The Chain Rule States That One “Differentiates The Outside, Leaving The Inside Alone, Then Differentiates The Inside Function.” The Derivative Of The Sin(X) With Respect To X Is The Cos(X), And The Derivative Of 2X With Respect To X Is Simply 2.

What Is a Derivative Of Cos 2X?

The Derivative Of Cos(2X) Is -2Sin(2X). The Process Of Finding This Derivative Uses The Chain Rule. We Can Use Integrals To Check Our Work When Finding Derivatives. If D(X) Is The Derivative Of F(X), Then The Integral Of D(X) Is F(X) + C, Where C Is A Constant.

What Is Formula Of Sin2X?

Double-angle Formulas: Sin 2X = 2Sin X Cos X, Cos 2X = Cos2X − Sin2X = 2Cos2X − 1=1 − 2Sin2X.